Introduction to Intervals
An interval is the distance between two pitches. Intervals can occur between pitches sounded one after another (melodic intervals) or between pitches sounded simultaneously (harmonic intervals). We will cover melody and harmony specifically in a later section, but for now we will consider the basic principles of intervals.
Accidentals, Half Steps, and Whole Steps
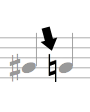

Sharps, flats, and natural signs (naturals) are collectively called accidentals. Accidentals alter pitches by moving them up or down by the smallest interval in the Western system: a half step. A sharp raises a pitch by a half step, a flat lowers a pitch by a half step, and a natural negates the effect of a sharp or flat sign, returning the note to its default pitch.
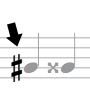
'h' stands for a half step, and 'W' stands for a whole step
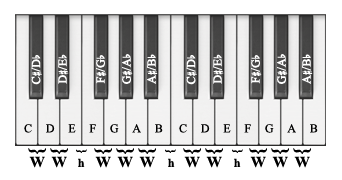
Let's look more closely at the half step. Using the keys of a piano as an example, notice that the interval between any white key and an adjacent black key is one half step (example: C and C-sharp ). But be careful! The interval between two white keys that do not have a black key between them (B and C , E and F ) is also a half step. In order to create a whole step, we need to go two half steps (example: C to D, E to F-sharp).
Half steps and whole steps are the building blocks for scales, which we will cover in a later section.
Enharmonic Equivalence

You may have noticed on the keyboard that all of the black keys are labeled with two pitch names (example: C-sharp/D-flat). This is a result of enharmonic equivalence, which is the principle that any pitch can have more than one name. C-sharp and D-flat, for example, are the same pitch. It is easy to think of them as musical homophones - they may be spelled differently, but they sound the same. Although they are not indicated on the keyboard shown here, it is also possible to have C-flat (same as B), B-sharp (same as C), F-flat (same as E), and E-sharp (same as F), but these are not very common. Double flats and sharps are also possible, and they simply raise or lower a pitch by two half steps (one whole step), but double accidentals are also uncommon.
Octaves

On the keyboard you can see that the pitches are named with seven letters of the alphabet: A, B, C, D, E, F, and G. There are only seven because they repeat, as on the white keys of the keyboard. An octave is the distance between any pitch and the next highest or lowest pitch of the same name (examples: D to D, F-sharp to F-sharp).
At first it may seem confusing that some pitches share the same name, but there is an acoustic principle recognized in all cultures that keeps the system orderly: octave equivalence. This is the principle that every pitch with the same name sounds like a higher or lower duplication of every pitch of that name. That is, every C sounds like a duplication of every other C, just higher or lower. This is because the frequencies of these notes are related by a 2:1 ratio. For example, the A above middle C occurs at 440 Hz, therefore the A one octave higher occurs at 880 Hz, and the A one octave lower occurs at 220 Hz.
In the example below you will hear examples of octave equivalence. First will be three examples of notes an octave apart, then you will hear a phrase from the American National Anthem played in two different octaves, first separately, then simultaneously. As you listen to the excerpt, notice that the melody from the National Anthem sounds equivalent - not identical but equivalent - in either octave. When both the higher and lower octave versions of the melody are played simultaneously, they are almost indistinguishable from each other.
Octaves
More Intervals
| Half Steps | Interval Name | Abbreviation |
| 0 | (Perfect) Unison | - |
| 1 | minor 2nd, half step | m2, h |
| 2 | Major 2nd, whole step | M2, W |
| 3 | minor 3rd | m3 |
| 4 | Major 3rd | M3 |
| 5 | Perfect 4th | P4 |
| 6 | tritone | tt |
| 7 | Perfect 5th | P5 |
| 8 | minor 6th | m6 |
| 9 | Major 6th | M6 |
| 10 | minor 7th | m7 |
| 11 | Major 7th | M7 |
| 12 | (Perfect) Octave | Oct, 8ve |
So far, we have discussed the half step, the whole step, and the octave. It is important to note that there are many other intervals that can be made between two pitches. For the sake of completeness, here is a chart showing the names and sizes (in half steps) of all the intervals that can occur within an octave. Note that the 4th and 5th are called 'perfect' rather than major or minor. In addition to the 4th and 5th, unisons and octaves are also considered perfect intervals. The reason for this label has to do with the harmonic series, so we will cover that in a later section.
For more on intervals, see intervals in major and minor scales and intervals in the chromatic scale.

